Bài tập trang 49,50 sgk toán 10

1. Xác định tọa độ của đỉnh và các giao điểm với trục tung, trục hoành (nếu có) của mỗi parabol.

a) y = x² - 3x + 2;                                         b) y = - 2x² + 4x - 3;

c) y = x² - 2x;                                               d) y = - x² + 4. 

Hướng dẫn.

a) a) y = x² - 3x + 2. Hệ số: a = 1, b = - 3, c = 2.

• Hoành độ đỉnh x₁ = 
• Tung độ đỉnh y₁ = 

          Vậy đỉnh parabol là .

• Giao điểm của parabol với trục tung là A(0; 2).
• Hoành độ giao điểm của parabol với trục hoành là nghiệm của phương trình:

 x² - 3x + 2 = 0 ⇔ x₁ = 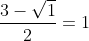, x₁ = . 

         Vậy các giao điểm của parabol với trục hoành là B(1; 0) và C(2; 0).

b) Đỉnh I(1; 1). Giao điểm với trục tung A(0;- 3).

Phương trình  - 2x² + 4x - 3 = 0 vô nghiệm. Không có giao điểm cuả parabol với trục hoành.

c) Đỉnh I(1;- 1). Các giao điểm với hai trục tọa độ: A(0; 0), B(2; 0).

d) Đỉnh I(0; 4). Các giao điểm với hai trục tọa độ: A(0; 4), B(- 2; 0), C(2; 0).

2. Lập bảng biến thiên và vẽ đồ thị của các hàm số.

a) y = 3x²- 4x + 1;                      b) y = - 3x² + 2x – 1;

c) y = 4x²- 4x + 1;                      d) y = - x² + 4x – 4;

e) y = 2x²+ x + 1;                       f) y = - x² + x - 1.

Hướng dẫn.

a) Bảng biến thiên: 

                            

Đồ thị: - Đỉnh: 

- Trục đối xứng: 

- Giao điểm với trục tung A(0; 1)

- Giao điểm với trục hoành , C(1; 0).

(hình dưới).

b) y = - 3x² + 2x – 1= 

Bảng biến thiên: 

Vẽ đồ thị: - Đỉnh  Trục đối xứng: .

               - Giao điểm với trục tung A(0;- 1).

               - Giao điểm với trục hoành: không có.

Ta xác định thêm mấy điểm: B(1;- 2), C(1;- 6). (bạn tự vẽ).

c) y = 4x² - 4x + 1 = .

Lập bảng biến thiên và vẽ tương tự câu a, b.

d) y = - x² + 4x – 4 = - (x – 2)²

Bảng biến thiên:

Cách vẽ đồ thị:

Ngoài cách vẽ như câu a, b, ta có thể vẽ như sau:

+ Vẽ đồ thị (P) của hàm số y = - x^2.

+ Tịnh tiến (P) song song với Ox sang phải 2 đơn vị được (P₁) là đồ thị cần vẽ. (hình dưới).

e), g) Bạn tự giải.

3. Xác định parabol y = ax² + bx + 2, biết rằng parabol đó:

a) Đi qua hai điểm M(1; 5) và N(- 2; 8);

b) Đi qua hai điểm A(3;- 4) và có trục đối xứng là x=

c) Có đỉnh là I(2;- 2);

d) Đi qua điểm B(- 1; 6) và tung độ của đỉnh là 

Hướng dẫn.

a) Vì parabol đi qua M(1; 5) nên tọa độ của M nghiệm đúng phương trình của parabol:  5 = a.1² + b.1 + 2.

Tương tự, với N(- 2; 8) ta có: 8 = a.(- 2)² + b.(- 2) + 2 

Giải hệ phương trình:  ta được a = 2, b = 1.

Parabol có phương trình là: y = 2x² + x + 2.

b) Giải hệ phương trình: 

Parabol: y = 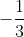 x² - x + 2.

c) Giải hệ phương trình: 

Parabol: y = x² - 4x + 2.

d) Ta có: 

Parabol: y = 16x² + 12x + 2 hoặc y = x² - 3x + 2.

4. Xác định a, b, c, biết parabol y = ax² + bx + c đi qua điểm A(8; 0) và có đỉnh I(6; - 12).

Hướng dẫn.

Ta có hệ phương trình: 

Parabol: y = 3x² - 36x + 96.